A confidence interval gives an estimated range of values which is likely to include an unknown population parameter eg the mean, the estimated range being calculated from a collected sample of data. The width of the confidence interval gives us some idea about how uncertain we are about the unknown parameter . A very wide interval may indicate that more data should be collected before anything very definite can be said about the parameter.
The only way you can really get a statistical parameter of a population with 100% confidence is to test the whole population. Generally the population is large and testing the whole population is costly and impracticable. However it is possible to use a sample and to calculate a range within which the population parameter value is likely to fall. Normally this is taken to be "95% likelyhood," and the range is called the 95% confidence interval. It is also possible to produce 90%, 99%, 99.9%, confidence intervals for the unknown parameters.
Symbols
| f(x) = probability function. (values between 0 and 1) F(x) = probability distribution function. Xm = Sample mean var = sample variance Φ (x) = Probability distribution function.(Standardised probability ) |
μ = population /random variable mean σ 2 = population /random variable variance σ = population /random variable standard deviation xm = arithmetic mean of sample sx 2 = variance of sample sx = Standard deviation of sample |
Confidence Interval ref.Normal Probability Distribution
It can be easily proved that for data that is "normally distributed" about 68.3% of the data will be within 1 standard deviation ( σ ) of the mean μ (i.e., within the range μ ± σ). In general there is a relationship between the fraction of the included data and the deviation from the mean in terms of standard deviations e.g the data fraction is related to μ ± c.σ) as shown in the table below
| Fraction of Data values | c |
| 50,0% | 0,674 |
| 68,3% | 1,000 |
| 90,0% | 1,645 |
| 95,0% | 1,960 |
| 95,4% | 2,000 |
| 98,0% | 2,326 |
| 99,0% | 2,576 |
| 99,7 | 3,000 |
Examples of data spread:
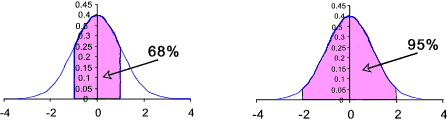
For a sample of a normal population one would expect about 68% of the values to be within ± 1.00 of the sample mean xm
For a sample of a normal population one would expect about 95% of the values to be within ± 1.96 of the sample mean xm.
Example 1:
A random variable is normally distributed with a standard deviation of 5. A random single sample from this distribution is 12,4 . Find the interval of values such that there is a 99% confidence that the population mean is with the interval range.
From the table above P(μ -2,58 σ < x < +2,58 σ ) = 0.99
Therefore P(μ -12,9 < x < + 12,9 )= 0.99
This implies P(12,4 -12,9 < μ < 12,4 -12,9 ) =0,99
That is -0,5 < μ < 25,3 = with 99% confidence.
This is simply stating that based on a single sampled value of 12,4 then there is a 99% confidence that the population mean is within the rang -0,5 to 25,3. This is a wide range and not very useful. To obtain a more smaller interval a larger sample, ( greater n ) is required. The distribution of the mean of this sample will be normally distribution with a variance of σ 2 /n (refer to notes below)
Example 2:
Obtain a 95% confidence interval for the mean of a normal distribution with a variance σ 2 = 9, i.e a standard deviation σ = 3
using a sample of n = 100 with a mean x m = 5:
For a 95% confidence interval c = 1,96.
The confidence interval for a 95% probability = P( xm - 1,96 .3 / √ 100 > μ ;> xm + 1,96 .3 / √ 100 > )
That is there is a 95% confidence that the mean of the population will be within 4,412 and 5,588
Background Theory
Sample distribution of a population mean
Consider a single random variable X
Now x 1....x n are observed values of X. The x i values can also be values of random variables X 1, X 2.. Xn. These have the same distributions as X but are independent because the sample values are independent.
Now it is clear that:
X = X 1 + X 2 +.......+X n
This is a normal distribution with a mean
μ = μ 1 + μ 2+....+μn
and a variance
σ 2 = σ 21 + σ 22+....+σ 2n
Considering a population with a mean μ and variance σ 2 .
Now taking a number of samples of size n from this population. Each sample has a mean x m and a variance s x .
It is useful obtain the distribution of the sample mean.

The mean of the sample distribution m (Xm ) = μ
The variance of the sample distribution mean var ( X m) = σ 2 / n
The Standard deviation of the sample distribution mean SD( X m) = σ / √ n
Central Limit Theorem
If X is a random variable with mean μ and variance σ 2 then the distribution of the sample mean approximates to a Normal distribution with mean μ and variance σ 2 /n as n --> ![]()
This is applicable for all distributions of X when n > 30
This is good for normal distribution for all values of n >0
The Central Limit theorem is the foundation for many statistical procedures, because the distribution of the population under study does not have to be Normal : the sample statistic will be tend to a normal distribution anyway.
This is very useful when it comes to inference e.g it permits hypothesis tests which assume normality even if the basis data seems to be non-normal( assuming reasonably large sample sizes. This is because the tests use the sample mean , which according to the Central Limit Theorem will be approximately normally distributed. Hypothesis Tests