Volume
Cy
Cz
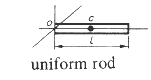
--
0,
0
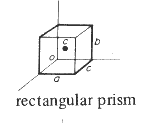
a.b.c
b/2 ,
c/2
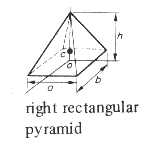
a.b.h /3
h/4,
0
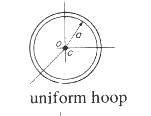
0
0,
0
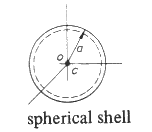
0
0,
0
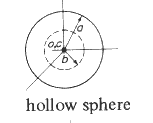
4.π. (a 3 - b 3 ) / 3
0,
0
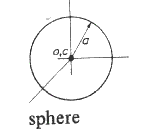
4.π .a 3 /3
0,
0
2.π .a 3 /3
3.a /8,
0

π.a 2 .h
π.a2 .h /3
h/4 ,
0
2.π.a.b.c /3
0 ,
0
h/2,
0
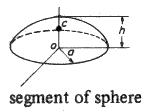
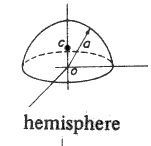
a = radius of sphere
π.h2 (r - h/3)
h.(4.a -h)/ 4.(3.a - h),
0


| Disclaimer: The information on this page has not been checked by an independent person. Use this information at your own risk. |
Click arrows to page adverts
Properties of Solids ShapesPoint at which the entire weight of a body may be considered as concentrated so that if supported at this point the body would remain in equilibrium in any position. If body is considered to be a particle then all of the mass or area is assumed to act at this point.
The Moment of Inertia quantifies the resistance of a physical object to angular acceleration. Moment of inertia is to rotational motion as mass is to linear motion.
In general, an object's moment of inertia depends on its shape and the distribution of mass within that shape: the greater the concentration of material away from the object's centroid, the larger the moment of inertia. The principal moments of inertia are miminum values with axes through the centroid. The parallel axes rule can be used to determine moments of inertia relative to displaced axes of rotation.
The radius with reference to an axis is that distance form the axis at which the entire mass of a body may be considered as concentrating keeping the moment of inertia unchanged.
I = m.ko2
Parallel Axis RuleTo determine the Moment of Inertia about an axis which is parallel to a centroid axis and at a distance d .
Iw = I + m.d2
NotesCx = centroid from yz plane....... Cy = centroid from xz plane....... Cz = centroid from xy plane..
I xx, I yy,I zz are the principal mass moments of inertia for axes through the centroid C in the direction x,y, & z.
 |
Area Volume |
Cx Cy Cz |
I xx | I yy | I zz |
 |
-- -- |
l /2 , 0, 0 |
0 | m.l 2 / 12 | m.l 2 / 12 |
 |
2.(a.b + a.c +b.c) a.b.c |
a/2 , b/2 , c/2 |
m. (b 2 + c2 ) /12 | m. (c 2 + a 2 ) /12 | m. (a 2 + b2 ) / 12 |
 |
--- a.b.h /3 |
0, h/4, 0 |
m (4.b 2 + 3.h 2 ) /80 | m (a 2 + b 2 ) /20 | m .(4.a 2 + 3.h 2 ) /80 |
 |
0 0 |
0, 0, 0 |
m.a 2 /2 | m.a 2 /2 | m.a 2 |
 |
4.π .a2 0 |
0, 0, 0 |
2.m.a 2 /3 | ||
 |
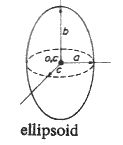
4.π .a 2 4.π. (a 3 - b 3 ) / 3 |
0, 0, 0 |
2.m.(a 5 - b 5) / 5.(a 3 - b 3) | ||
 |
4.π .a2 4.π .a 3 /3 |
0 , 0, 0 |
2.m.a 2 /5 | ||
 |
2.π.a2 2.π .a 3 /3 |
0, 3.a /8, 0 |
-- | 2.m.a2 /5 | -- |
 |
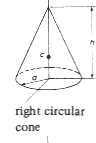
2.π.a.( h + a ) π.a 2 .h |
0, h/2 , 0 | m.(3.a 2 + h 2 )/12 | m.a 2 /2 | m.(3.a 2 + h 2 )/12 |
 |
π.a.(Sqrt(a 2 + h 2)+a) π.a2 .h /3 |
0, h/4 , 0 |
3.m.(4.a 2 + h 2 )/80 | 3. m.a 2 / 10 | 3.m.(4.a 2 + h 2 )/80 |
 |
--- 2.π.a.b.c /3 |
0 , 0 , 0 |
m.(b 2 + c 2 )/5 | m.(c 2 + a 2 )/5 | m.(a 2 + b 2 )/5 |
 |
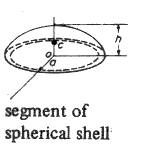
2.π.r.h |
0, h/2, 0 |
-- | -- | -- |
 a = radius of sphere |
2. π.r.h π.h2 (r - h/3) |
0 , h.(4.a -h)/ 4.(3.a - h), 0 |
 |
 |
|
Links to Properties of Figures
|
|
Send Comments to Roy Beardmore
Last Updated 01/05/2010